<<< règles du jeu
All the pawns are reversible, being white on one side and black on the other. This is because they can be captured and flipped as the game progresses.
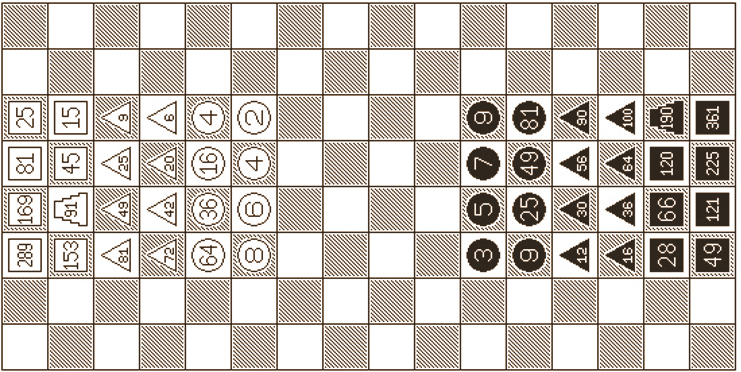
The Black Pyramid is made up of a "64" Square, a "49" Square, a "36" Triangle, a "25" Triangle, and a "16" Round, which adds up to the Pyramid's value of 190.
These irregular values make it hard for them to be captured by most of the capturing methods listed below, except for Siege.
Pyramids can move like a Round, a Triangle, or a Square, as long as they still contain the respective piece, which makes them very valuable.
Components
- A 16 by 8 chessboard
- 57 pawns, 29 black ones and 28 white ones, broken down as follows:
Black Pieces
- 8 round pieces, of values: 3 - 5 - 7 - 9 - 9 - 25 - 49 - 81 (odd numbers 3 to 9 and their squares)
- 8 triangular pieces, of values: 12 - 30 - 56 - 90 - 16 - 36 - 64 - 100 (3*4 / 5*6 / 7*8 / 9*10 and the squares of 4 - 6 - 8 - 10)
- 7 square pieces, of values: 28 - 66 - 120 - [190] - 49 - 121 - 225 - 361 (4*7 / 6*11 / 8*15 / [10*19] and the squares of 7 - 11 - 15 - 19)
- the preceding 190 pieces are broken down into a pyramid of: round 16 (4*4), triangular 25 (5*5), triangular 36 (6*6), square 49 (7*7), square 64 (8*8)
White Pieces
- 8 round pieces, of values: 2 - 4 -6 - 8 - 4 - 16 - 36 - 64 (even numbers 2 to 8 and their squares)
- 8 triangular pieces, of values: 6 - 20 - 42 - 72 - 9 - 25 - 49 - 81 (2*3 / 4*5 / 6*7 / 8*9 and the squares of 3 / 5 / 7 / 9)
- 7 square pieces, of values: 15 - 45 - 153 - 25 - 81 - 169 - 289 (3*5 / 5*9 / [7*13] / 9*17 and the squares of 5 / 9 / 13 / 17) (note that 3+2=5 / 5+4=9 / 7+6=13 / 9+8=17)
- the preceding 91 piece is broken down into a pyramid of: round 1 (1*1), triangular 9 (3*3), triangular 16 (4*4), square 25 (5*5), square 36 (6*6)
All the pawns are reversible, being white on one side and black on the other. This is because they can be captured and flipped as the game progresses.
Moves of pieces
- Rounds: Rounds move one square in any of the four diagonals.
- Triangles: Triangles can move exactly two squares vertically or horizontally, but not diagonally.
- Squares: Squares can move exactly three squares vertically or horizontally, but not diagonally.
- Pyramids: Pyramids are not actually one piece, but more than one piece put together.
The Black Pyramid is made up of a "64" Square, a "49" Square, a "36" Triangle, a "25" Triangle, and a "16" Round, which adds up to the Pyramid's value of 190.
These irregular values make it hard for them to be captured by most of the capturing methods listed below, except for Siege.
Pyramids can move like a Round, a Triangle, or a Square, as long as they still contain the respective piece, which makes them very valuable.
Set up
Common Victories:
- by body: If a player captures a certain number of pieces set by both players, he wins the game.
- by goods: If a player captures enough pieces to add up to or exceed a certain value that is set by both players, he wins the game.
- by lawsuit: If a player captures enough pieces to add up to or exceed a certain value that is set by both players, and the number of digits in his captured pieces' values are less than a number set by both players, he wins the game.
- by honour: If a player captures enough pieces to add up to or exceed a certain value that is set by both players, and the number of pieces he captured are less than a certain number set by both players, he wins the game.
- by honour and lawsuit: If a player captures enough pieces to add up to or exceed a certain value that is set by both players, the number of digits in his captured pieces' values are less than a number set by both players, and the number of pieces he captured are less than a certain number set by both players, he wins the game.
Proper Victories:
- Great victory: This occurs when three pieces that are arranged are in an arithmetic progression.
- Greater victory: This occurs when four pieces that are arranged have three pieces that are in a certain progression, and another three pieces that are in another type of progression.
- Most excellent victory: This occurs when four pieces that are arranged have all three types of mathematical progressions in three different groups.
Victory Conditions
Both players must agree, when starting a game, on which victory conditions to use. There are seven common victories and seven proper victories.
The Common Victories are:
- The Victory of Body: To take a set number of pawns
- The Victory of Assets: To take a set total value in pawns
- The Victory of Proceeds: To take a set number of digits
- The Victory of Body and Assets
- The Victory of Body and Proceeds
- The Victory of Assets and Proceeds
- The Victory of Body, Assets, and Proceeds
- Mediocre Victories,
- Great Victories, and
- Excellent Victory
In an Arithmetic Progression, the differences between successive numbers are given by a single value (called the ratio of the progression). For example: 2 - 5 - 8 - 11 is an Arithmetic Progression of ratio 3.
In a Geometric Progression, the ratios between successive numbers are given by a single value (called the ratio of the progression). For example: 3 - 12 - 48 is a Geometric Progression of ratio 4.
In an Harmonic Progression, the ratio of two successive differences is equal to the ratio of the end numbers. If the Progression is a - b - c, we have c/a = (c-b)/(b-a). This number is the progression's ratio. For example: 4 - 6 - 12 is an Harmonic Progression of ratio 3, as 12/4 = 3 and (12-6)/(6-4) = 6/2 = 3.
The Mediocre Victories are achieved by obtaining one of the progressions. The Great Victories are achieved by obtaining two progressions at once. The Excellent Victory is achieved by obtaining all three progressions at once.
Movement
There are two types of moves: Regular and Irregular. In a Regular move, the piece slides from its starting point to its end point; the intervening squares must be unobstructed. In an Irregular move, the piece jumps from its starting point to its end point, regardless of obstacles.Round piece movement template (* Regular, + Irregular)
Triangular piece movement template (* Regular, + Irregular)
Square piece movement template (* Regular, + Irregular)
Captures
Captures must precede or follow a Regular move. When the capture precedes the move, the capturing pawn takes the captured pawn's place. When the capture follows the move, the captured pawn's place is left empty. It is possible to achieve several captures at once, both before and after the move! When capturing several pawns before a move, the capturing pawn chooses which captured pawn's place to take. Captures are NOT mandatory. Captured pawns are flipped and may be re-introduced on the board, on any free square of the player's board edge. Putting a captured pawn down replaces a move. It is possible to capture in this way.
There are six ways to capture:
1. The Encounter
The capturing pawn comes within one Regular move of the victim.B1: Round red D3: Square black. If white moves his piece to C2, he could capture black.
2. The Ambush
When a number is equal to the sum, difference, product, or ratio of two opposing pawns, it can be taken on condition that both capturing pawns be within a Regular move of the victim.B1, A4: Round black C2: Triangular red. If black moves his 4 to B3, he can take the 12 as 8+4=12 and both his pieces are within a Regular move of the red piece.
3. The Assault
A number encounters an opposing pawn in the same row, column, or diagonal so that the number of intervening squares is equal to their product or ratio. The intervening squares must be unoccupied.D1: Triangular red B3: Round black A4: Triangular black. By moving his 2 out of the way (to A2 or C4), black captures white as 12/6=2, the number of intervening squares.
4. The Power
When a number is equal to one of the powers or roots of an opposing pawn, the latter can be taken on condition that the capturing pawn be within a Regular move of the victim.
B1: Round red B3: Square black. If the 3 is moved to A2 or C2, it can take 81 as 3 is the fourth root of 81.
5. The Progression
When a number can be made part of an Arithmetic, Geometric, or Harmonic progression with at least two opposing pawns, it can be taken on condition that both capturing pawns be within a Regular move of the victim.A1: Round red D1: Square black C3: Triangular black. If black moves his 20 to A3, he can take the 25 as 15-20-25 is an Arithmetic progression (of ratio 5) and both his 15 and 20 will be within a Regular move of the 25.
6. The Emprisonment
If a pawn is so surrounded that it cannot accomplish a Regular move, it can be captured.
B2: Triangular red D4: Triangular black. If black moves his 72 to B4, he imprisons the red 30 as all of his possible Regular moves will then be blocked by black or red pawns.
Pyramids
Pyramids can be taken apart one component pawn at a time, or all at once. A pyramid's value is given, at all times, by the sum of the values of its component pieces. The pyramid can itself capture, using either its total value, or the value of any one of its component pieces. The only restriction is that it cannot dislocate itself when moving.